In practice, embeddings with a fixed size are not always optimal. For some tasks, embeddings may be too large, which can increase the computational complexity of the model in general. For other tasks, smaller embeddings can decrease the model's accuracy. At the same time, retraining the model for each task can be very time-consuming and costly.
The authors of the paper under consideration propose a new approach to training neural networks that allows them to generate embeddings with different dimensions on-the-fly. With Matryoshka Representation Learning (MRL), we can train a model once and then use embeddings of different sizes depending on the specific task at hand.
The key idea
Let us define \( d \) – the size of the embedding. We can extract nested subspaces of sizes \( \frac{d}{2}, \frac{d}{4}, \frac{d}{8}, \frac{d}{16} ..., \) and train the model so that embedding from each subspace would be a good independent embedding in terms of the problem being solved.
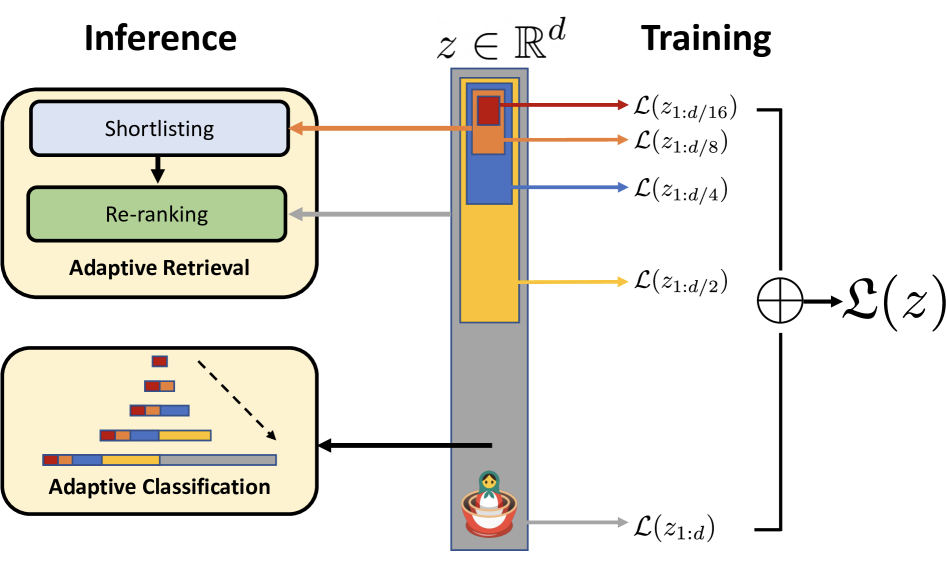
In MRL, the authors modified the training procedure in such a way that the first \( m (m < d) \) elements of the embedding of the size \( d \) contained common and transferable to other tasks representations.
In this paper, the image classification and retrieval tasks have been solved. Therefore, the resulting loss function for neural network training is the sum of Cross Entropy losses with Softmax for each nested subspace, where each subspace uses its own linear classifier.
The authors also noted that we can share weights between linear classifiers for different subspaces. In experiments, they demonstrated that this approach works, and called it Efficient Matryoshka Representation Learning (MRL-E). MRL-E produces worse results than "standard" MRL, but it does not incur additional computational costs during model training.
Experiments
The authors of the work did not select the best hyperparameters in their experiments, but took them from baselines. To evaluate the effectiveness of their training strategy, they tested it on four tasks: classification, adaptive classification, retrieval and adaptive retrieval. Next, I will briefly describe the main results of these experiments.
Classification
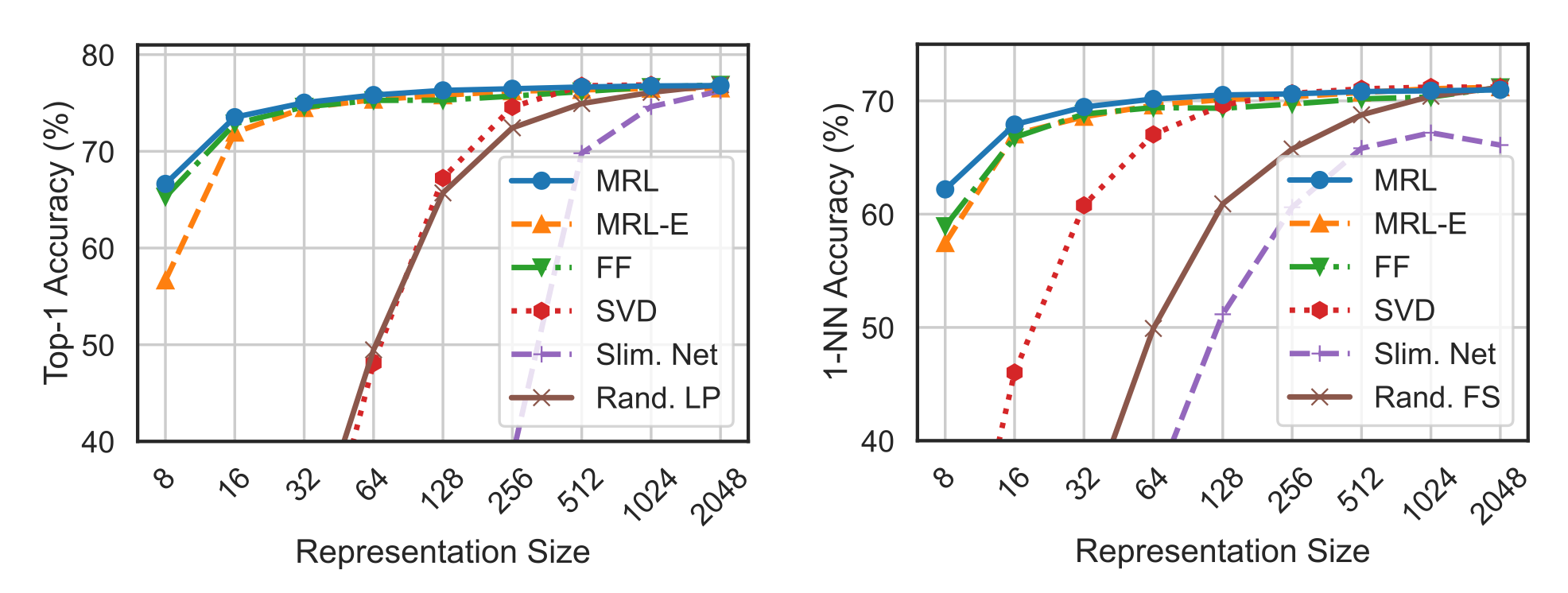
The authors chose the following models for comparison:
- FF – independently trained low-dimensional representations
- SVD – the size of embeddings is reduced by SVD
- Slimmable Networks
- Rand. LP – randomly selected features of the highest capacity FF model
Next, the authors evaluated the quality of classification on the ImageNet dataset using linear classification and 1-nearest neighbor. MRL showed the best results: with a small embedding size, the quality is even slightly higher than for fixed embeddings of the same size, and significantly better than both randomly selected features and SVD. Additionally, it is also worth noting that the "optimized" MRL-E also performed quite well.
Adaptive classification
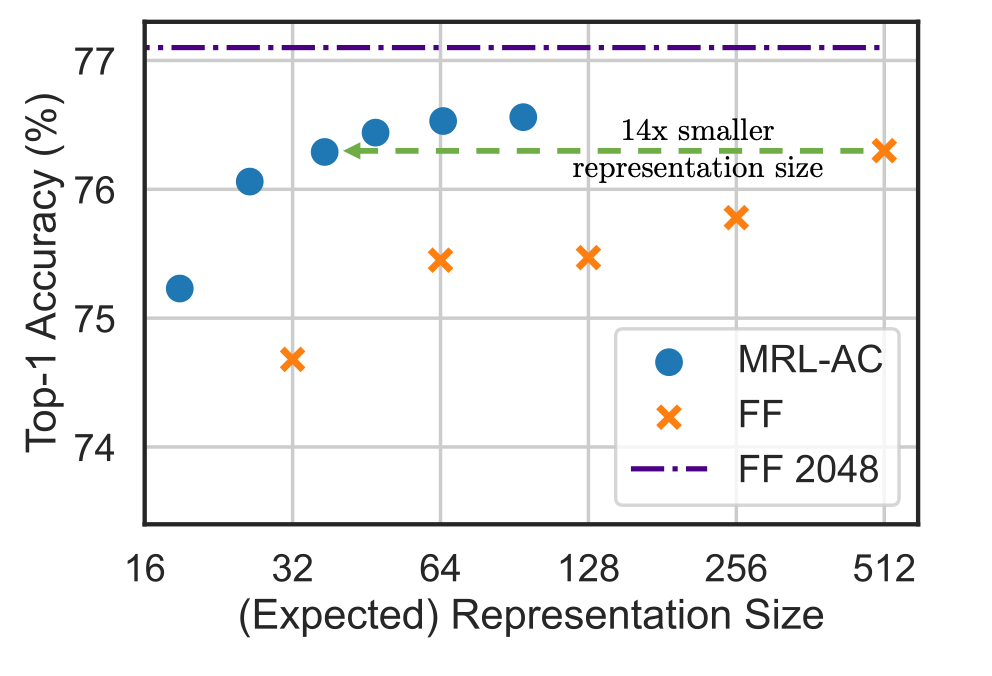
Since a model trained using the strategy proposed in this work can produce embeddings of several dimensions at once, it is possible to do adaptive classification with cascades. For example, we start with the smallest embedding, get a prediction, and if confidence is below the threshold, we use the next largest embedding. As a result, the authors showed that in this way, it is possible to achieve quality comparable to large embedding of a fixed size while reducing the dimension by 14 times.
Retrieval and adaptive retrieval
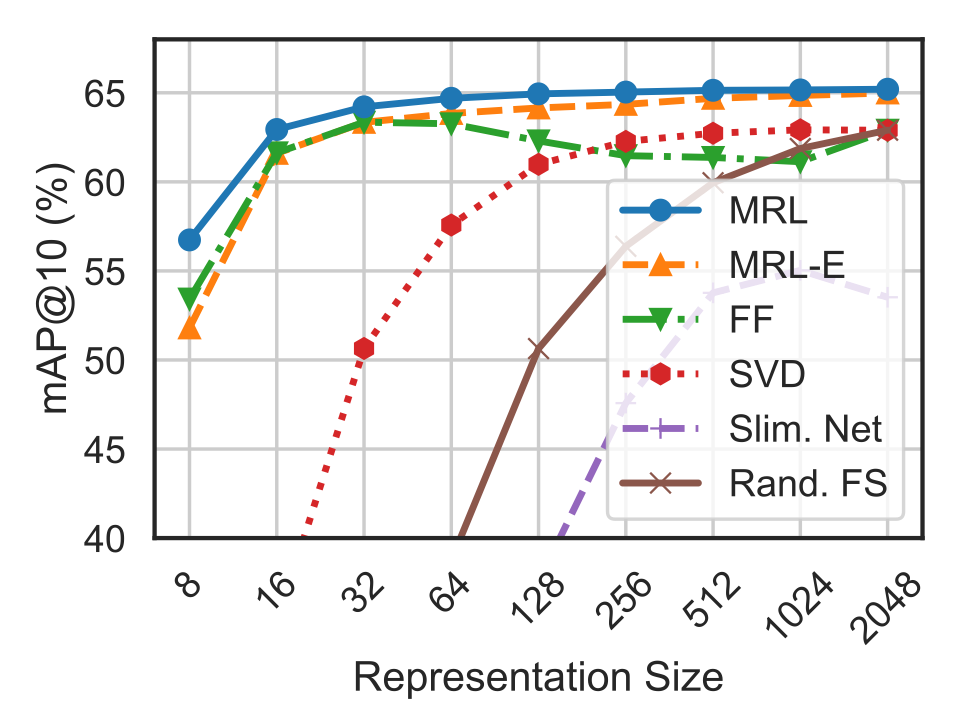
The retrieval task is to use the query image to find images of the same class in the database. This is done by pairwise comparing embeddings. To evaluate quality, the mean Average Precision@10 (mAP@10) metric is used. In the authors' experiments, MRL performs better than baselines.
But in my opinion, the most interesting results are obtained in the adaptive retrieval (AR) task. Due to the proposed training strategy, we can save a lot of space without storing large embeddings. In AR, we first receive a shortlist of candidates through a low-dimensional embedding, then the list is reranked through a higher-dimensional embedding. This procedure is much less computationally expensive than direct neighbor search using higher-dimensional embedding. Theoretically, this approach is 128 times more efficient and produces results comparable to direct neighbor search using high-dimensional embedding.
Conclusion
The proposed Matryoshka Representation Learning strategy has a lot of practical applications. In my opinion, the main advantage of this work is the ability to significantly reduce the computational costs of classification (adaptive classification), matching and searching in the database (adaptive retrieval).

My thesis is indirectly confirmed by OpenAI. Last month they added an embedding size selection feature that uses MRL. Interestingly, with this feature, the text-embedding-3-large model with low-dimensional embeddings performs better than previous versions of this model with higher-dimensional embeddings.







